Integrated Analysis with Python: XGBoost, SHAP, and GeoShapley
- 10 Aug 2025
- Acadmic Method, Machine Learning
- by alasbahimoha
Summary
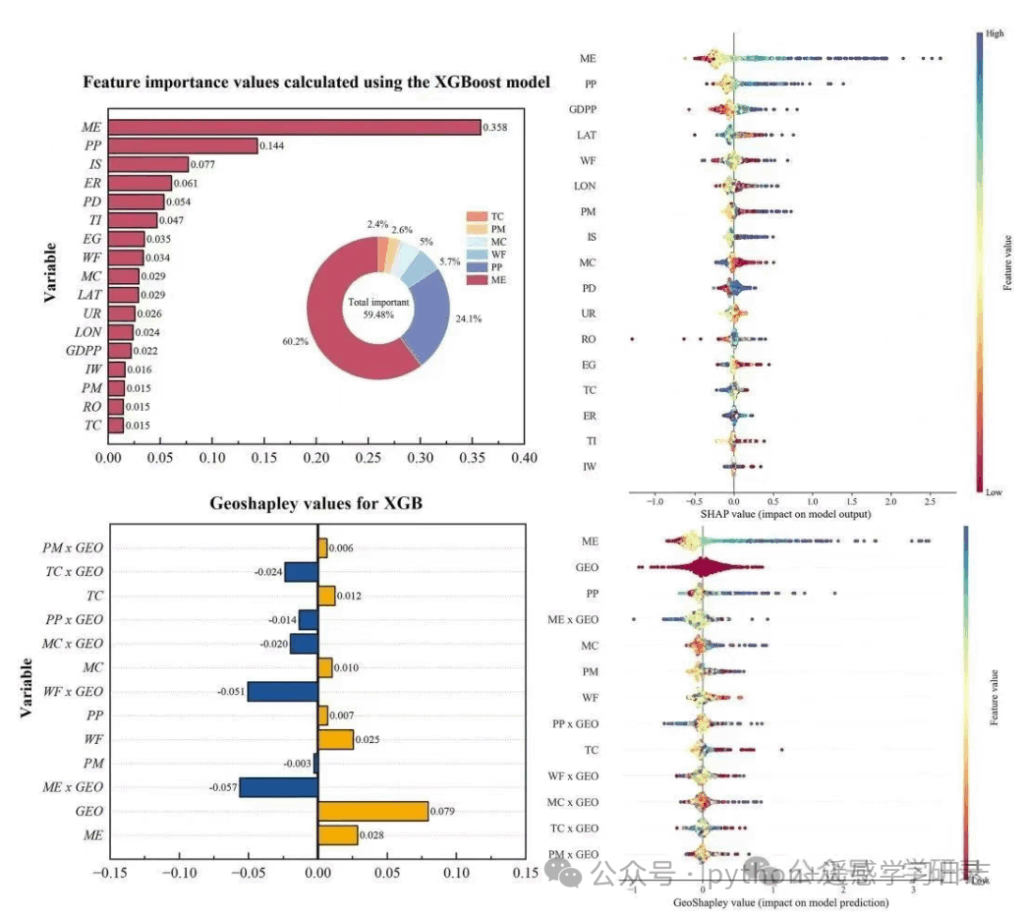
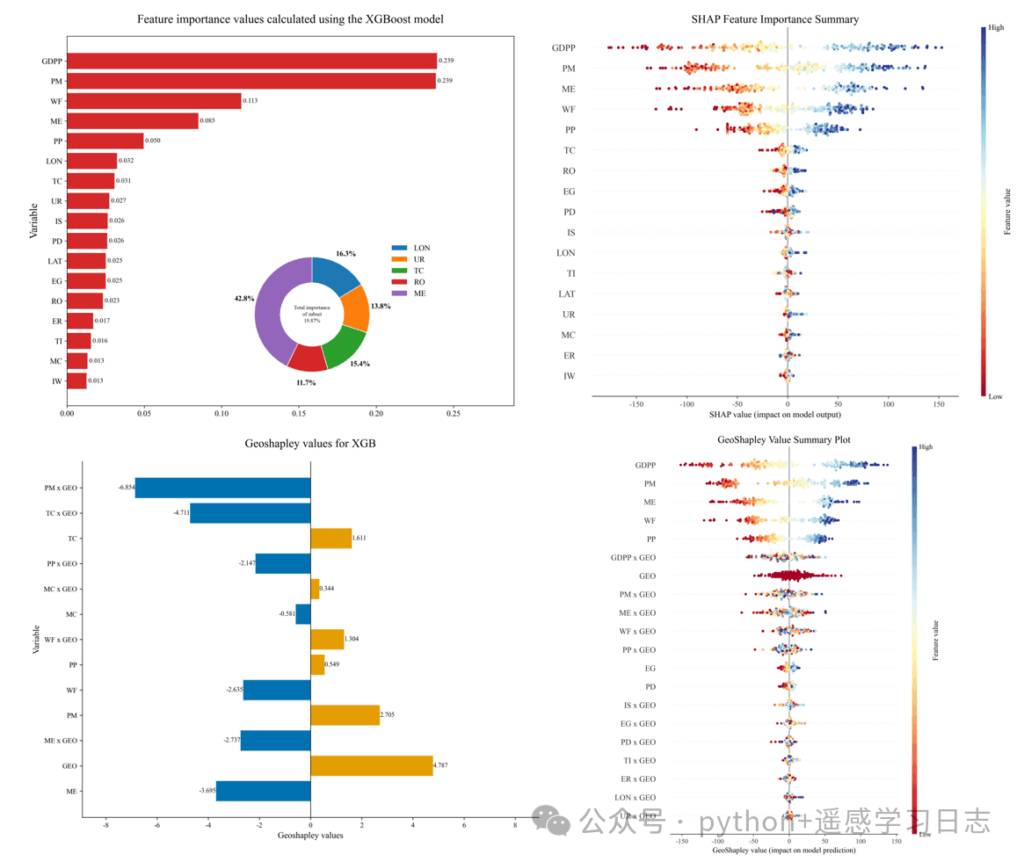
This tutorial reproduces the XGBoost + SHAP + GeoShapley integrated analysis method (as used in a Journal of Cleaner Production article) using Python. We first train an XGBoost model on a tabular dataset, then probe the model’s decision mechanism using three lenses: the model’s native feature_importances_, global and local explanations via SHAP values, and spatially aware attributions via GeoShapley, with a particular focus on (i) how geographic variables contribute to predictions and (ii) how geography interacts with other features.
Workflow
- Data loading & preprocessing
- XGBoost model training
- SHAP analysis
- GeoShapley analysis
Results
Reference paper: Yan Chen, Sheng Jiao, Xinyue Gu, Shan Li. Decoding the spatiotemporal effects of industrial clusters on carbon emissions in a Chinese river basin. Journal of Cleaner Production, 2025, 516, 145851.
Reproducible Simulation
Below is the end-to-end code (broken into sections) followed by detailed explanations of what each part does and why.
What you need installed
- Python 3.9+
pandas,numpy,matplotlib,scikit-learn,xgboost,shap,geoshapley- Install with:
pip install pandas numpy matplotlib scikit-learn xgboost shap geoshapley
1) Environment setup & global plotting style
# ===== 1. Imports and global style =====
import pandas as pd
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import xgboost as xgb
from sklearn.model_selection import train_test_split
import shap
from geoshapley import GeoShapleyExplainer
# (Optional) If you run this in a desktop Python session and need a GUI backend:
# matplotlib.use('TkAgg')
# ---- Global style ----
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.sans-serif'] = ['Times New Roman', 'SimHei'] # Fallback for Chinese labels
plt.rcParams['axes.unicode_minus'] = False # Show minus signs correctly
Why this matters
- We import everything we’ll use: data handling (
pandas,numpy), plotting (matplotlib), modeling (xgboost), train/test split (sklearn), and explainability (shap,geoshapley). - The font settings keep figures readable and avoid the infamous “square minus sign” issue.
2) Data loading
# ===== 2. Load your data from Excel =====
print("--- Step 1: Loading data from Excel ---")
# >>> Replace this path with YOUR actual file path <<<
excel_path = r'model_simulation_results.xlsx'
# The Excel is assumed to contain a 'target' column (the prediction target)
# and feature columns, including two geographic coordinate columns 'LAT' and 'LON'
# (rename later if yours differ).
df_full_dataset = pd.read_excel(excel_path)
# Split features and target
df_features = df_full_dataset.drop(columns=['target'])
y = df_full_dataset['target']
# Keep feature names for plots
feature_names = df_features.columns.tolist()
print(f"Data loaded successfully with {len(feature_names)} features.")
What happens here
- We read an Excel file into a DataFrame.
- We separate the target (what we want to predict) from the features (inputs to the model).
- Assumptions you can change:
- The target column is called
target. - Latitude/longitude columns are
LATandLON. If your data uses different names (e.g.,lat_dd,lon_dd), you’ll edit those names in the GeoShapley section.
- The target column is called
3) XGBoost model training
# ===== 3. Train an XGBoost regressor =====
print("\n--- Step 2: Training XGBoost model ---")
X_train, X_test, y_train, y_test = train_test_split(
df_features, y, test_size=0.2, random_state=42
)
model = xgb.XGBRegressor(
n_estimators=100,
max_depth=5,
learning_rate=0.1,
objective='reg:squarederror',
random_state=42
)
model.fit(X_train, y_train)
print("Model training complete.")
Rationale for the hyperparameters
n_estimators=100: number of trees to grow. More trees capture more patterns but can overfit; tune in practice.max_depth=5: moderate tree depth to balance bias/variance.learning_rate=0.1: typical starting point; lower values often need more trees.objective='reg:squarederror': squared error loss for regression. For classification, you’d choose a different objective.
4) Feature importance + visualization
# ===== 4. Feature importance (model-native) & donut inset =====
print("\n--- Step 3: Extracting feature importances and plotting ---")
importances = model.feature_importances_
df_importance = pd.DataFrame({
'feature': feature_names,
'importance': importances
}).sort_values('importance', ascending=True)
fig, ax = plt.subplots(figsize=(12, 10))
bars = ax.barh(df_importance['feature'], df_importance['importance'],
color='#d62828', label='Importance')
ax.set_title('Feature importance values calculated using the XGBoost model', fontsize=18, pad=20)
ax.set_ylabel('Variable', fontsize=16)
ax.tick_params(axis='both', which='major', labelsize=12)
for bar in bars:
width = bar.get_width()
ax.text(width, bar.get_y() + bar.get_height()/2,
f' {width:.3f}', va='center', ha='left', fontsize=10)
ax.set_xlim(right=ax.get_xlim()[1] * 1.15)
# ---- Optional donut for a chosen subset of features ----
donut_features = ['LON', 'UR', 'TC', 'RO', 'ME'] # edit to match names present in your data
df_donut = df_importance[df_importance['feature'].isin(donut_features)].copy()
if not df_donut.empty and df_donut['importance'].sum() > 0:
df_donut['feature'] = pd.Categorical(df_donut['feature'],
categories=donut_features, ordered=True)
df_donut = df_donut.sort_values('feature')
total_donut_importance = df_donut['importance'].sum()
donut_percentages_raw = df_donut['importance'] / total_donut_importance * 100
ax_inset = fig.add_axes([0.4, 0.15, 0.3, 0.3])
colors = matplotlib.colormaps.get('tab10').colors
wedges, texts = ax_inset.pie(
donut_percentages_raw,
colors=colors[:len(df_donut)], startangle=90, counterclock=False,
wedgeprops=dict(width=0.45, edgecolor='w')
)
subset_importance_ratio = df_donut['importance'].sum() / df_importance['importance'].sum()
ax_inset.text(0, 0, f'Total importance\nof subset\n{subset_importance_ratio:.2%}',
ha='center', va='center', fontsize=8, linespacing=1.5)
label_threshold = 2.0
y_text_offsets = {'left': 1.4, 'right': 1.4}
for i, p in enumerate(wedges):
percent = donut_percentages_raw.iloc[i]
ang = (p.theta2 - p.theta1)/2 + p.theta1
y = np.sin(np.deg2rad(ang))
x = np.cos(np.deg2rad(ang))
if percent < label_threshold and percent > 0:
side = 'right' if x > 0 else 'left'
y_pos = y_text_offsets[side]
y_text_offsets[side] += -0.2 if y > 0 else 0.2
connectionstyle = f"angle,angleA=0,angleB={ang}"
ax_inset.annotate(f'{percent:.1f}%', xy=(x, y),
xytext=(0.1*np.sign(x), y_pos),
fontsize=10, ha='center',
arrowprops=dict(arrowstyle="-", connectionstyle=connectionstyle))
elif percent > 0:
ax_inset.text(x*1.2, y*1.2, f'{percent:.1f}%',
ha='center', va='center', fontsize=11, fontweight='bold')
ax_inset.legend(wedges, df_donut['feature'], loc="center left",
bbox_to_anchor=(1, 0.8), frameon=False, fontsize=12)
plt.savefig('feature.jpg', dpi=300, bbox_inches='tight')
plt.show()
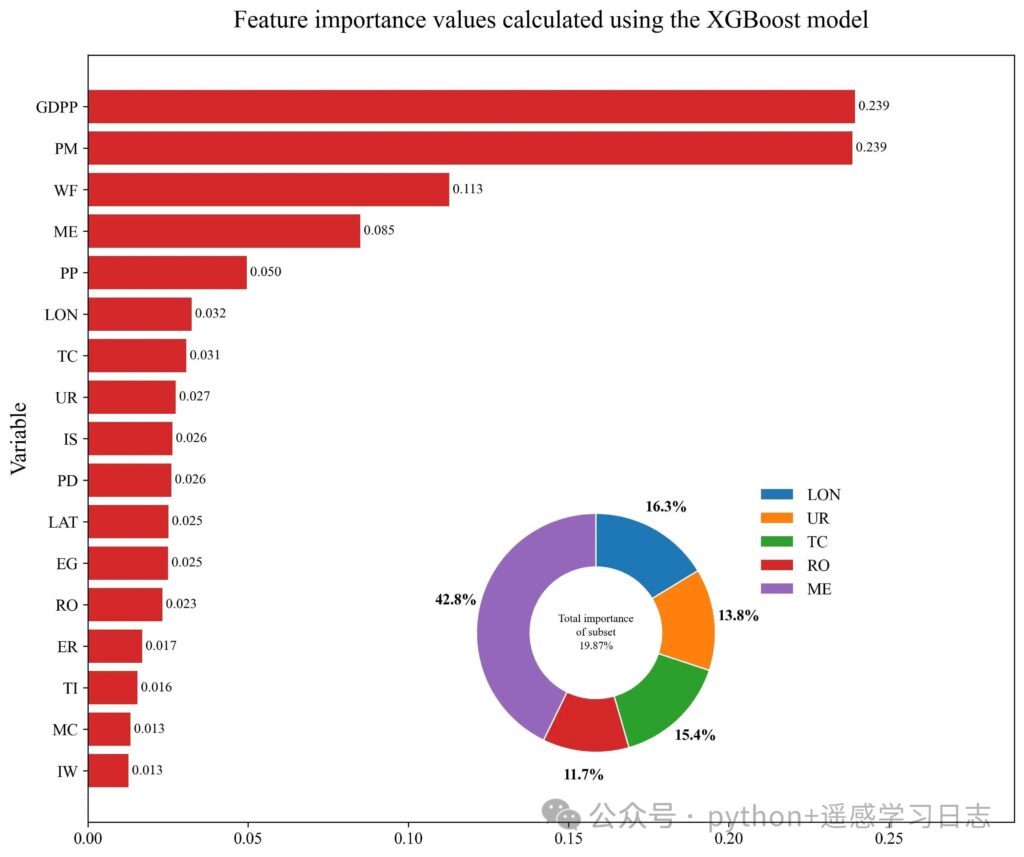
Interpretation
The donut inset shows the relative share of a hand-picked subset of features within that subset (not the whole model), which is useful when you want to highlight geography-related variables or a thematic group.
The horizontal bars rank features by model-native importance (gain/weight/cover depending on booster; for xgboost’s scikit wrapper, this defaults to the booster’s importance type).
5) SHAP analysis
# ===== 5. SHAP analysis =====
print("\n--- Step 4: Running SHAP analysis and plotting ---")
# A fast TreeExplainer for tree ensembles; baseline is inferred from the model
explainer = shap.TreeExplainer(model)
# Compute SHAP values for the whole dataset (consider subsampling for large data)
shap_values = explainer(df_features)
plt.figure(figsize=(10, 8))
shap.summary_plot(
shap_values, df_features,
plot_type="dot", cmap="RdYlBu",
show=False, plot_size=None
)
ax2 = plt.gca()
ax2.set_title("SHAP Feature Importance Summary", fontsize=16)
ax2.set_xlabel("SHAP value (impact on model output)", fontsize=12)
plt.savefig('SHAP_summary_plot.jpg', dpi=300, bbox_inches='tight')
print("\n--- SHAP summary plot saved to: SHAP_summary_plot.jpg ---")
plt.show()
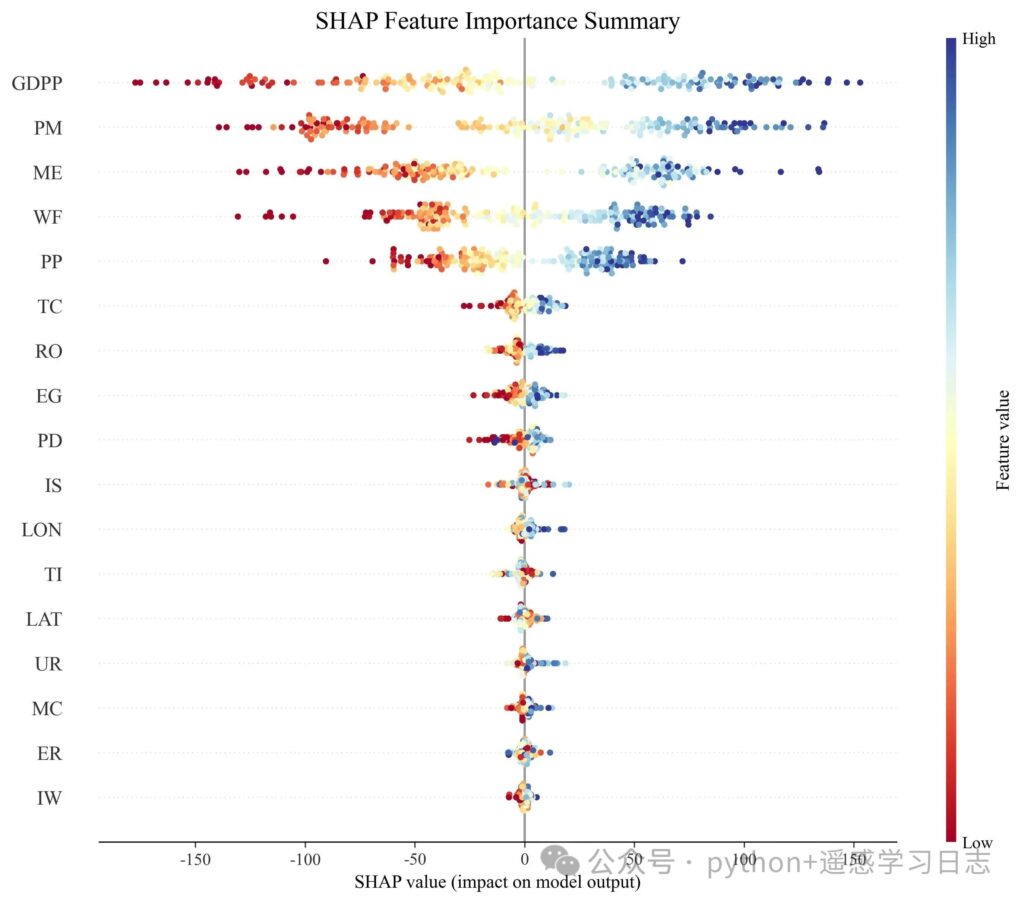
What this shows
- Each row is a feature, sorted by global impact (mean |SHAP|).
- Each dot is a sample’s local contribution of that feature.
- Color encodes the original feature value (red = high, blue = low by default).
- Reading left→right: how much that feature pushes the prediction up or down for that sample.
Why SHAP complements feature_importances_
- Native importance is aggregate and can be biased by collinearity or tree split mechanics.
- SHAP gives signed, local attributions and a consistent global ranking derived from them.
6) GeoShapley analysis
# ===== 6. GeoShapley analysis =====
print("\n--- Step 5: Running GeoShapley analysis ---")
# 6.1 Prepare background and run
background_data = df_features.sample(100, random_state=42).values
data_to_explain = df_features # you can also pass X_test for speed
geoshap_explainer = GeoShapleyExplainer(model.predict, background_data)
print("GeoShapley computing... (single-core)")
geoshapley_results = geoshap_explainer.explain(data_to_explain, n_jobs=1)
print("GeoShapley analysis complete.")
# 6.2 Aggregate effects and build a diverging bar plot
print("\n--- Step 6: Aggregating results and plotting diverging bars ---")
# >>> If your coordinate column names differ, change them here <<<
coord_columns = ['LAT', 'LON']
non_spatial_features = [f for f in feature_names if f not in coord_columns]
# Mean effects across samples
mean_primary = pd.Series(
geoshapley_results.primary.mean(axis=0),
index=non_spatial_features
)
mean_interaction = pd.Series(
geoshapley_results.geo_intera.mean(axis=0),
index=[f'{f} x GEO' for f in non_spatial_features]
)
mean_spatial = pd.Series(
geoshapley_results.geo.mean(),
index=['GEO']
)
df_plot = pd.concat([mean_primary, mean_interaction, mean_spatial]).reset_index()
df_plot.columns = ['Variable', 'Value']
# Customize the order to match your narrative; example below:
vars_to_show = [
'PM x GEO', 'TC x GEO', 'TC', 'PP x GEO', 'MC x GEO', 'MC',
'WF x GEO', 'PP', 'WF', 'PM', 'ME x GEO', 'GEO', 'ME'
]
df_plot = df_plot[df_plot['Variable'].isin(vars_to_show)]
df_plot['Color'] = ['#e69f00' if x >= 0 else '#0072b2' for x in df_plot['Value']]
df_plot['Variable'] = pd.Categorical(df_plot['Variable'],
categories=vars_to_show, ordered=True)
df_plot = df_plot.sort_values('Variable', ascending=False)
fig3, ax3 = plt.subplots(figsize=(10, 8))
ax3.barh(df_plot['Variable'], df_plot['Value'], color=df_plot['Color'])
for _, row in df_plot.iterrows():
value = row['Value']
ha = 'left' if value > 0 else 'right'
offset = 0.002 if value > 0 else -0.002
ax3.text(value + offset, row['Variable'], f'{value:.3f}',
ha=ha, va='center', fontsize=9)
ax3.axvline(x=0, color='black', linewidth=0.8)
ax3.set_title('GeoShapley values for XGB', fontsize=16, pad=20)
ax3.set_xlabel('GeoShapley values', fontsize=12)
ax3.set_ylabel('Variable', fontsize=12)
ax3.spines['top'].set_visible(False)
ax3.spines['right'].set_visible(False)
current_xlim = ax3.get_xlim()
max_abs_lim = max(abs(current_xlim[0]), abs(current_xlim[1]))
ax3.set_xlim(-max_abs_lim * 1.2, max_abs_lim * 1.2)
plt.tight_layout()
plt.savefig('geoshapley_final_plot.jpg', dpi=300)
plt.show()
print("\n--- All analyses and plots completed successfully ---")
# ===== 6b. Built-in beeswarm summary plot =====
print("\n--- Step 7: Built-in GeoShapley beeswarm summary ---")
plt.figure(figsize=(10, 8))
geoshapley_results.summary_plot(include_interaction=True, cmap='RdYlBu')
ax2 = plt.gca()
ax2.set_title("GeoShapley Value Summary Plot", fontsize=16)
ax2.set_xlabel("GeoShapley value (impact on model prediction)", fontsize=12)
plt.savefig('geoshapley_beeswarm_plot_colored.jpg', dpi=300, bbox_inches='tight')
plt.show()
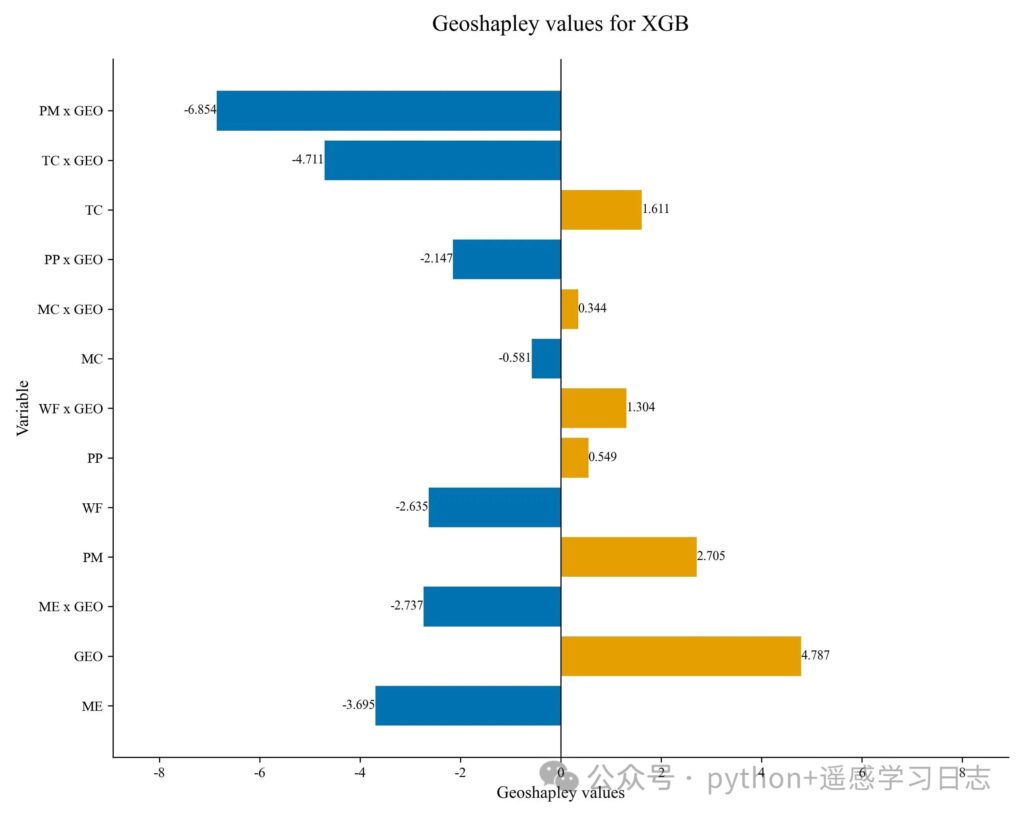
How to read the diverging bars
- Primary (main) effects of non-spatial features (e.g.,
TC,MC) show how much each feature contributes independently of location. - Geo interaction effects (e.g.,
TC x GEO) quantify how much location modulates the effect of that feature. Positive bars: on average, the feature’s effect is amplified by geography; negative bars: dampened or reversed. - GEO alone is the pure geographic effect (location’s direct contribution that is not attributed to any single non-spatial feature).
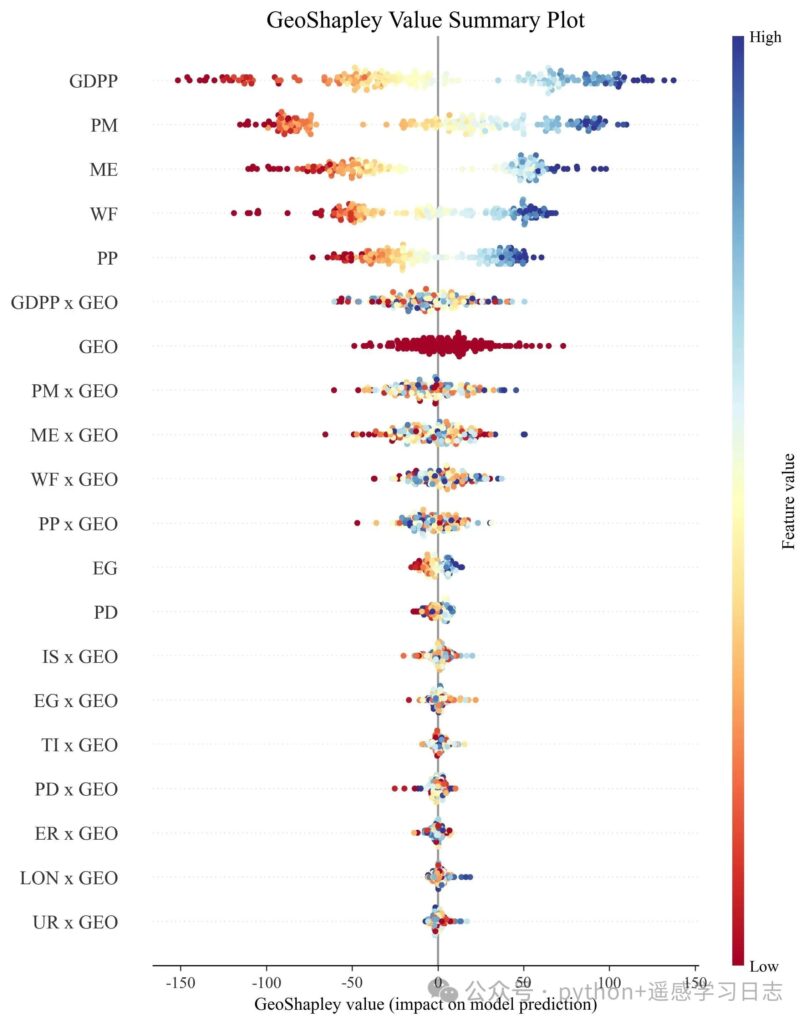
GeoShapley beeswarm
- The y-axis lists all effect terms (main effects, interactions with GEO, and the pure
GEOeffect), sorted by mean absolute GeoShapley. - Each point is a sample; the x-axis is that sample’s GeoShapley value (signed contribution).
- Color reflects the underlying feature’s raw value for main/interaction effects, or the most related feature for
GEO(as defined by the algorithm).
Notes, Tips, and Common Pitfalls
Paths
- Update every file path (Excel input, image outputs) to valid locations on your machine.
Runtime
- GeoShapley can be slow on large data or many features.
- You can increase
n_jobsingeoshap_explainer.explain(..., n_jobs=<cores>)if your machine has more cores. - Consider explaining only a subset (e.g.,
X_test) to iterate faster.
- You can increase
Coordinate columns
- This tutorial assumes your spatial coordinates are stored in columns
'LAT'and'LON'. Changecoord_columns = ['LAT', 'LON']if needed.
Why three lenses (complementarity)
- XGBoost importances: quick global ranking, but can be biased by tree structure.
- SHAP: consistent, local-to-global attributions; great for understanding feature effects and value-dependent behavior.
- GeoShapley: explicitly decomposes main, geo-interaction, and pure geographic effects—crucial for spatial modeling where “where” you are may change “how” features act.